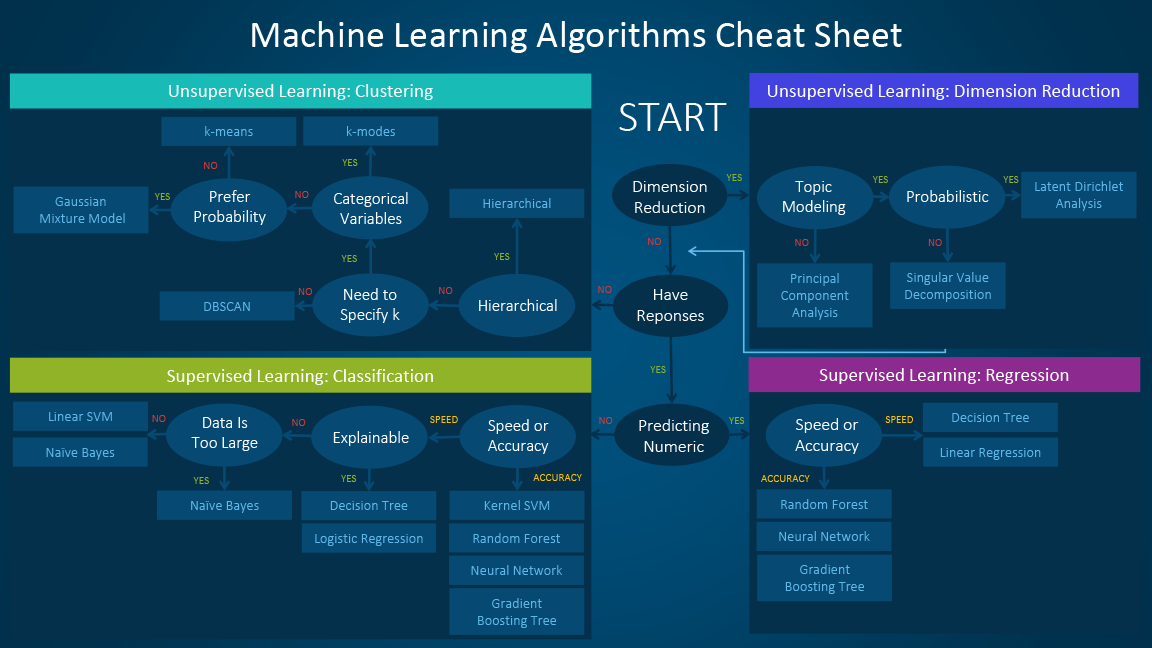
Topics¶
- Supervised vs. Unsupervised learning
- K means
- Gaussian Mixture Model
- DBSCAN
Supervised / Unsupervised Learning¶
Unsupervised learning:
- Just dataset, no targets or labels
- Algorithm needs to "make sense" of the data itself
- E.g. clustering, dimension reduction
Supervised learning:
- Dataset with targets or labels
- Algorithm learns by minimizing loss against the targets / labels
- E.g. Classification, regression
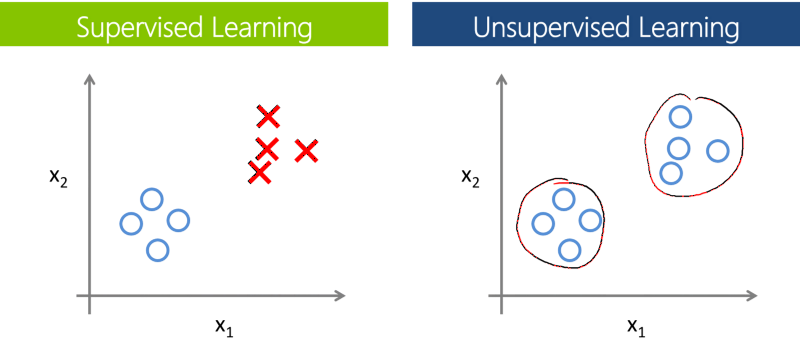
(image: Vibhor Agarwal)
Clustering¶
Objective: given a dataset with just features, find groups (or clusters) of them
Broad applications:
- Market segmentation
- User recommendations
- Anormaly detection
Algorithms¶
- K-means / K-modes
- Expectation Maximization / Gaussian Mixture
- DBSCAN
Comparison: http://scikit-learn.org/stable/modules/clustering.html#overview-of-clustering-methods
K-means¶
- Divides $N$ samples into $K$ clusters $C$
- Each cluster is centered on a mean $\mu_j$, known as a "centroid"
- Objective is to minimize "inertia" (= within-cluster sum-of-squares)
$$\sum_{i=0}^n \underset{\mu_j \in C} {\arg \min}{(\|x_i - \mu_j\|^2)}$$
http://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html
Workshop: K-means clustering¶
Dataset: COE Bidding Results¶
https://data.gov.sg/dataset/coe-bidding-results
- Download the dataset on your machine
- Extract into a folder and note the path for use in
pd.read_csv
import pandas as pd
df = pd.read_csv('D:/tmp/coe-bidding-results/coe-results.csv', # fix to your path
usecols=['month', 'vehicle_class', 'quota', 'premium'],
parse_dates=['month'])
df.month
0 2010-01-01
1 2010-01-01
2 2010-01-01
3 2010-01-01
4 2010-01-01
5 2010-01-01
6 2010-01-01
7 2010-01-01
8 2010-01-01
9 2010-01-01
10 2010-02-01
11 2010-02-01
12 2010-02-01
13 2010-02-01
14 2010-02-01
15 2010-02-01
16 2010-02-01
17 2010-02-01
18 2010-02-01
19 2010-02-01
20 2010-03-01
21 2010-03-01
22 2010-03-01
23 2010-03-01
24 2010-03-01
25 2010-03-01
26 2010-03-01
27 2010-03-01
28 2010-03-01
29 2010-03-01
...
955 2017-12-01
956 2017-12-01
957 2017-12-01
958 2017-12-01
959 2017-12-01
960 2018-01-01
961 2018-01-01
962 2018-01-01
963 2018-01-01
964 2018-01-01
965 2018-01-01
966 2018-01-01
967 2018-01-01
968 2018-01-01
969 2018-01-01
970 2018-02-01
971 2018-02-01
972 2018-02-01
973 2018-02-01
974 2018-02-01
975 2018-02-01
976 2018-02-01
977 2018-02-01
978 2018-02-01
979 2018-02-01
980 2018-03-01
981 2018-03-01
982 2018-03-01
983 2018-03-01
984 2018-03-01
Name: month, Length: 985, dtype: datetime64[ns]
# Check that the month is read correctly (should be datetime64[ns])
df.dtypes
month datetime64[ns] vehicle_class object quota int64 premium int64 dtype: object
# Get a subset of dates where the distribution is less variable
df = df[(df.month >= '2016') & (df.month < '2017') ]
# see how many entries, and their ranges
df.describe()
| quota | premium | |
|---|---|---|
| count | 120.000000 | 120.000000 |
| mean | 875.858333 | 41509.191667 |
| std | 702.687928 | 18090.047866 |
| min | 162.000000 | 6012.000000 |
| 25% | 359.250000 | 43751.250000 |
| 50% | 449.500000 | 48152.000000 |
| 75% | 1394.500000 | 52751.000000 |
| max | 2272.000000 | 58201.000000 |
Task¶
Find clusters using the
quota, andpremiumcolumns.Compare the clusters found with the actual
vehicle_classlabel
Note: in unsupervised learning, we DON'T provide the label for training the algorithm
Data Processing¶
- Take the last 300 samples for demo purposes
- Encode labels from ['Category A', ...] to [0, 1, 2, ...]
- Shuffle and split the data into train and test
- Scale the data
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder, StandardScaler
# For demo purposes, use the first 300 samples
n_samples = 300
df = df.iloc[:n_samples]
df_data = df.loc[:, 'quota':'premium']
# Encode labels
le = LabelEncoder()
df_labels = le.fit_transform(df.loc[:, 'vehicle_class'])
# Train, test split, and shuffle
df_data_train, df_data_test, df_labels_train, df_labels_test = train_test_split(df_data, df_labels)
# Scale the data to simplify processing
scaler = StandardScaler()
scaler.fit(df_data_train)
df_data_train_scaled = scaler.transform(df_data_train)
df_data_test_scaled = scaler.transform(df_data_test)
print('Labels\n', df_labels_train[:5])
print('Data\n', df_data_train_scaled[:5])
Labels [4 4 2 4 1] Data [[-0.39942055 0.35565315] [-0.58391406 0.46452395] [-0.97135042 0.38250175] [-0.46328369 0.89590608] [ 0.22927654 0.49667666]]
Helper functions¶
Here's a helper function to visualize the k-means algorithm.
It does this:
- For the min-max ranges of
quotaandpremium(after scaling), runKmeans.predictto get the label outputs [0, 1, 2, 3, 4] (for 5 categories) - Plot a colour mesh, with colour assigned to each label
- Scatter plot the training data in black
- Scatter plot the centroids in red
import numpy as np
def plot_decision_boundaries(ax, title, kmeans_model, data):
"""Plots the decision boundaries for a fitted k-means model
Args:
ax: subplot axis
title: subplot title
kmeans_model: a fitted sklearn.cluster.KMeans model
data: 2-dimensional input data to cluster and plot
Based on: http://scikit-learn.org/stable/auto_examples/cluster/plot_kmeans_digits.html
"""
# Step size of the mesh. Decrease to increase the quality of the VQ.
h = .02 # point in the mesh [x_min, x_max]x[y_min, y_max].
# Plot the decision boundary. For that, we will assign a color to each
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Obtain labels for each point in mesh using the trained model.
Z = kmeans_model.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.imshow(Z, interpolation='nearest',
extent=(xx.min(), xx.max(), yy.min(), yy.max()),
cmap=plt.cm.Pastel2,
aspect='auto', origin='lower')
ax.plot(data[:, 0], data[:, 1], 'k.', markersize=4)
# Plot the centroids as a red X
centroids = kmeans.cluster_centers_
ax.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='red', zorder=10, label='centroids')
ax.set(title=title,
xlim=(x_min, x_max), ylim=(y_min, y_max),
xticks=(), yticks=())
ax.legend()
Train and plot progress¶
Now we'll run k-means with different iterations.
Observe how the centroids move as the algorithm makes progress.
%matplotlib inline
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# Run k-means iteratively and plot to demonstrate the algorithm at work
n_classes = len(df.loc[:, 'vehicle_class'].unique())
n_iterations = [1, 5, 10, 20]
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
for n, ax in zip(n_iterations, axes.flatten()):
kmeans = KMeans(init='random', n_clusters=n_classes, max_iter=n, n_init=1)
kmeans.fit(df_data_train_scaled)
plot_decision_boundaries(ax, 'K-means, %d iteration(s)' % n, kmeans, df_data_train_scaled)
Exercise¶
Repeat the above, trying different options for k-means:
- Try a different initialization method:
k-means++ - Try averaging over different centroid seeds by setting
n_initto a number greater than 1 - Try a different algorithm:
full,elkan
You can run KMeans? to see its documentation.
# Your code here
Evaluating Clustering Algorithms¶
When you have the ground truth labels:
- Homogeniety: each cluster contains only members of 1 class
- Completeness: all members of 1 class are assigned to the same cluster
- V-measure: harmonic mean of homogeniety and completeness $$v\_measure = \frac{2 * homogeniety * completeness}{homogeniety+completeness}$$
- Adjusted Rand index: similarity measure, ignoring ordering
Adjusted Rand index¶
$$R = \frac{a+b}{a+b+c+d} = \frac{a+b}{{n \choose 2 }}$$
where:
- $a+b$: count of agreements between $X$ and $Y$
$c+d$: count of disagreements between $X$ and $Y$.
The probability that $X$ and $Y$ will agree on a randomly chosen pair (0: complete disagreement, 1: clusters are exactly the same).
The adjusted Rand index is the corrected-for-chance version of the Rand index. Though the Rand Index may only yield a value between 0 and 1, the adjusted Rand index can yield negative values if the index is less than the expected index.
Evaluating Clustering Algorithms¶
When you don't have the ground truth labels:
- Silhouette Coefficient
$$S = \frac{b-a}{max(a, b)}$$
Where:
- $a$: Mean distance between 1 sample and others in same class
- $b$: Mean distance between 1 sample and others in nearest clusters
Evaluating Clustering Algorithms¶
Advantages and disadvantages of each metric: http://scikit-learn.org/stable/modules/clustering.html#clustering-performance-evaluation
Workshop: Evaluating K-means on the COE dataset¶
Since we have our labels, we can evaluate the performance of the clustering algorithm using all of the above.
Higher numbers are better.
from sklearn import metrics
# Let's run to the maximum iterations
kmeans = KMeans(init='random', n_clusters=n_classes, max_iter=100, n_init=1)
kmeans.fit(df_data_train_scaled)
# Run prediction on the test data
test_labels_predict = kmeans.predict(df_data_test_scaled)
test_labels_predict
array([2, 0, 4, 0, 4, 0, 0, 3, 0, 4, 2, 0, 0, 3, 2, 4, 3, 0, 3, 4, 0, 4,
0, 1, 3, 3, 0, 2, 0, 2])
print("Homogeneity: %0.3f"
% metrics.homogeneity_score(df_labels_test, test_labels_predict))
print("Completeness: %0.3f"
% metrics.completeness_score(df_labels_test, test_labels_predict))
print("V-measure: %0.3f"
% metrics.v_measure_score(df_labels_test, test_labels_predict))
print("Adjusted Rand-Index: %.3f"
% metrics.adjusted_rand_score(df_labels_test, test_labels_predict))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(df_data_test_scaled, test_labels_predict,
sample_size=n_samples,
metric='euclidean'))
Homogeneity: 0.830 Completeness: 0.933 V-measure: 0.878 Adjusted Rand-Index: 0.718 Silhouette Coefficient: 0.461
Exercise¶
Compare the Evaluation Metrics for the different k-means settings you tried in the earlier exercise.
- A different initialization method: k-means++
- Averaging over different centroid seeds by setting n_init to a number greater than 1
- A different algorithm: full, elkan
Use max_iter = 100 or a similar value.
Which combination performs the best on this dataset?
# Your code here
Gaussian Mixture Models¶
Gaussian mixture models use the normal distribution
- Means are centered around clusters
- Assigns probabilities that a sample belongs to a cluster
http://scikit-learn.org/stable/modules/mixture.html#gaussian-mixture
Multivariate Gaussians¶
This section provides more background on Multivariate Gaussian distributions.
Univariate Gaussian¶
First, the univariate (i.e. single variable) Gaussian or normal distribution:
$$ \mathcal{N}(x: \mu, \sigma) = {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}exp\bigl[{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\bigr] $$
mean: $$\mu = \frac{1}{N}\sum_{i}^{N}{x_i}$$
variance: $$\sigma^2 = \frac{1}{N}\sum_{i}^{N}{(x_i - \mu)}^2$$
def plot_gaussian_1d(x, mean, sigma):
"""Plots a 1D Gaussian distribution
Args:
x: plotting range
mean: mean of the gaussian distribution
sigma: standard deviation of the gaussian distribution
"""
from scipy.stats import norm
# the location (loc) keyword specifies the mean.
# the scale (scale) keyword specifies the standard deviation.
z = norm.pdf(x, loc=mean, scale=sigma)
fig, ax = plt.subplots()
ax.plot(x, z)
ax.set(title='1D gaussian, $\mu$: %.2f, $\sigma$: %.2f' % (mean, sigma),
xlabel='x', ylabel='Gaussian')
ax.grid()
plt.show()
x = np.arange(-5, 5, .01)
mean = 0
sigma = 1
plot_gaussian_1d(x, mean, sigma)
mean = -1.
sigma = 1.
plot_gaussian_1d(x, mean, sigma)
mean = 1.
sigma = 2.
plot_gaussian_1d(x, mean, sigma)
mean = 1
sigma = 0.5
plot_gaussian_1d(x, mean, sigma)
Multivariate Gaussian¶
$$ \mathcal{N}(\vec{x}: \vec{\mu}, \Sigma) = \frac{1}{\sqrt{(2\pi)^d|\Sigma|}}exp\bigl[-\frac{1}{2}(\vec{x} - \vec{\mu})^T\Sigma^{-1}(\vec{x} - \vec{\mu})\bigr] $$
Mean vector (length d): $$\vec{\mu} = \frac{1}{N}\sum_{i=1}^{N}{\vec{x}_i}$$
Covariance matrix (d x d): $$\Sigma = \frac{1}{N}\sum_{j}^N(\vec{x}_i - \vec{\mu})^T(\vec{x}_i - \vec{\mu})$$
Compare (Univariate case):¶
$$ \mathcal{N}(x: \mu, \sigma) = {\frac {1}{\sqrt {2\pi \sigma ^{2}}}}exp\bigl[{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}\bigr] $$
mean: $$\mu = \frac{1}{N}\sum_{i=1}^{N}{x_i}$$
variance: $$\sigma^2 = \frac{1}{N}\sum_{i=1}^{N}{(x_i - \mu)}^2$$
Covariance Matrix¶
Covariance indicates the level to which two variables vary together.
From the multivariate normal distribution, we draw d-dimensional samples, $X = [x_1, x_2, ... x_d]$ and determine their covariance $\Sigma$
The element $\Sigma_{ij}$ is the "covariance" of $x_i$ and $x_j$ (i.e. the variance between samples in dimensions i and j)
The element $\Sigma_{ii}$ is the variance of $x_i$ (i.e. the "spread" in dimension i alone).
Types of Covariance Matrix:¶
- Spherical covariance (a multiple of the identity matrix)
$$ \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix} $$
- Diagonal covariance (has non-negative elements, and only on the diagonal)
$$ \begin{bmatrix} 4 & 0 \\ 0 & 100 \end{bmatrix} $$
Properties of Covariance Matrix:¶
must be positive semi-definite, because these are sums of squares. https://en.wikipedia.org/wiki/Positive-definite_matrix
must be invertible, because variance is non-zero
https://math.stackexchange.com/questions/1479483/when-does-the-inverse-of-a-covariance-matrix-exist
Reference: https://docs.scipy.org/doc/numpy/reference/generated/numpy.random.multivariate_normal.html
from mpl_toolkits.mplot3d import Axes3D
def plot_gaussian_2d(X, Y, mu, Sigma):
"""Plots a 2D Gaussian distribution
Args:
X: plotting range (dimension 1)
Y: plotting range (dimension 2)
mu: mean vector
Sigma: covariance matrix
"""
# scipy.stats.multivariate_normal generates
# the distribution;
# whereas numpy.random.multivariate_normal draws
# random samples from the distribution.
from scipy.stats import multivariate_normal
# pack X and Y into a single 3-dimensional array
# to pass into multivariate_normal
pos = np.empty(X.shape + (2,))
pos[:, :, 0] = X
pos[:, :, 1] = Y
f = multivariate_normal(mu, Sigma)
Z = f.pdf(pos)
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111, projection='3d')
# create a surface plot
ax.plot_surface(X, Y, Z, rstride=3, cstride=3, linewidth=1,
cmap=plt.cm.magma)
# project a contour plot under the surface plot
plot_offset = -0.2 # projection offset
cset = ax.contour(X, Y, Z, zdir='z', offset=plot_offset,
cmap=plt.cm.magma)
# plot the mean on the contour plot
ax.scatter(mu[0], mu[1], plot_offset, marker='x', color='r',
label='gaussian mean')
# adjust the limits, ticks, title, axes
ax.set(zlim=(plot_offset, 0.2), zticks=np.linspace(0, 0.2, 5),
xlabel='x1', ylabel='x2', zlabel='Gaussian',
title='2D gaussian: $\mu$: {}\n$\Sigma$: {}'.format(mu, Sigma))
# view angle
ax.view_init(27, -21)
ax.legend()
plt.show()
x = np.arange(-5, 5, .1)
y = np.arange(-5, 5, .1)
x, y = np.meshgrid(x, y)
# mean vector and covariance matrix
mu = np.array([0., 0.]) # zero centered
Sigma = np.eye(2) # 2x2 identity matrix (spherical)
plot_gaussian_2d(x, y, mu, Sigma)
# mean vector and covariance matrix
mu = np.array([2., -2.]) # shift to bottom left
Sigma = 2 * np.eye(2) # wider spherical
plot_gaussian_2d(x, y, mu, Sigma)
mu = np.array([-2., 2.]) # shift to top right
Sigma = .5 * np.eye(2) # narrower spherical
plot_gaussian_2d(x, y, mu, Sigma)
mu = np.array([0., 0])
Sigma = np.array([[.5, 0], [0, 2]]) # diagonal (x2 dominant)
plot_gaussian_2d(x, y, mu, Sigma)
mu = np.array([0., 0])
Sigma = np.array([[2, 0], [0, .5]]) # diagonal (x1 dominant)
plot_gaussian_2d(x, y, mu, Sigma)
mu = np.array([0., 0])
Sigma = np.array([[1., .6], [.6, 1.]])
plot_gaussian_2d(x, y, mu, Sigma)
Covariance Matrix Types (sklearn)¶
The covariance matrix type controls how the gaussian models are "mixed" together.
- Spherical: all components have spherical covariance matrices
- Diagonal: each component has its own axis-aligned covariance matrix
- Tied: all components have the same covariance matrix
- Full: all components can have different covariance matrix
Visualization: http://www.stats.ox.ac.uk/~sejdinov/teaching/dmml/Mixtures.html
Workshop: Gaussian Mixture Model on the COE dataset¶
In this workshop, we will apply GMMs to cluster the COE dataset.
# Credits: https://github.com/scikit-learn/scikit-learn/blob/master/examples/mixture/plot_gmm_pdf.py
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import LogNorm
from sklearn.mixture import GaussianMixture
def plot_gmm(ax, title, gmm, data):
"""Plots a Gaussian Mixture Model as a contour plot
Args:
ax: subplot axis
title: plot title
gmm: fitted Gaussian Mixture Model
data: data samples
"""
h = 0.1
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# negative log-likelihood scores for each point in the mesh
# using the trained model
Z = -gmm.score_samples(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# https://matplotlib.org/2.0.1/examples/pylab_examples/contour_demo.html
cax = ax.contour(xx, yy, Z,
levels=np.logspace(0, 3, 10),
colors=('red', 'orange', 'yellow', 'green', 'blue', 'indigo', 'violet'))
plt.colorbar(cax, shrink=0.8, extend='both', ax=ax)
ax.scatter(data[:, 0], data[:, 1], color='black', marker='x')
# plot the means (centers of the 5 Gaussian components)
means = gmm.means_
ax.scatter(means[:, 0], means[:, 1], marker='x',
s=169, linewidths=3, color='red', zorder=10, label='Gaussian means')
ax.legend(loc='lower right')
ax.set(title=title, xlim=(x_min, x_max), ylim=(y_min, y_max))
%matplotlib inline
n_classes = len(df.loc[:, 'vehicle_class'].unique())
covariance_types = ['spherical', 'diag', 'tied', 'full']
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(20, 20))
for cov_type, ax in zip(covariance_types, axes.flatten()):
gmm = GaussianMixture(n_components=n_classes, covariance_type=cov_type)
gmm.fit(df_data_train_scaled)
plot_gmm(ax, 'Negative log-likelihood predicted by a GMM (covariance type = %s)' % cov_type,
gmm, df_data_train_scaled)
def plot_gmm_3d(ax, title, gmm, data):
"""Plots a Gaussian Mixture Model as a 3D plot
Args:
ax: subplot axis
title: plot title
gmm: fitted Gaussian Mixture Model
data: data samples
"""
h = 0.1
x_min, x_max = data[:, 0].min() - 1, data[:, 0].max() + 1
y_min, y_max = data[:, 1].min() - 1, data[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
# negative log-likelihood scores for each point in the mesh
# using the trained model
score = gmm.score_samples(np.c_[xx.ravel(), yy.ravel()])
Z = score.reshape(xx.shape)
z_min, z_max = score.min() - 1, score.max() + 1
colors = ('red', 'orange', 'yellow', 'green', 'blue', 'indigo', 'violet')
ax.plot_surface(xx, yy, Z, rstride=8, cstride=8, alpha=0.3)
# use -Z to match the 2D plot
cax = ax.contour(xx, yy, -Z, zdir='z', offset=z_min, levels=np.logspace(0, 3, 10),
colors=colors)
ax.contour(xx, yy, Z, zdir='x', offset=x_min, cmap=plt.cm.spring)
ax.contour(xx, yy, Z, zdir='y', offset=y_min, cmap=plt.cm.autumn)
# plot the scatter points
ax.scatter(data[:, 0], data[:, 1], z_min, color='black', marker='x')
# plot the means (centers of the 5 Gaussian components)
means = gmm.means_
ax.scatter(means[:, 0], means[:, 1], z_min, marker='x',
s=169, linewidths=3, color='red', zorder=100,
label='Gaussian means')
plt.colorbar(cax, shrink=0.8, extend='both', ax=ax)
ax.set_xlabel('quota scaled')
ax.set_xlim(x_min, x_max)
ax.set_ylabel('premium scaled')
ax.set_ylim(y_min, y_max)
ax.set_zlabel('log likelihood')
ax.set_zlim(z_min, z_max)
ax.legend()
%matplotlib inline
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111)
cov_type = 'spherical'
gmm = GaussianMixture(n_components=5, covariance_type=cov_type)
gmm.fit(df_data_train_scaled)
plot_gmm(ax, 'Negative log-likelihood predicted by a GMM (covariance type = %s)' % cov_type,
gmm, df_data_train_scaled)
print(gmm.means_)
print(gmm.covariances_)
[[-0.94760802 0.31360055] [ 0.62758747 0.61875968] [-0.68721548 -1.89480595] [ 1.71698916 0.49373234] [-0.56123089 0.61286652]] [0.00982101 0.0412706 0.0007347 0.03301211 0.02918094]
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(15, 15))
ax = fig.add_subplot(111, projection='3d')
cov_type = 'spherical'
gmm = GaussianMixture(n_components=5, covariance_type=cov_type)
gmm.fit(df_data_train_scaled)
plot_gmm_3d(ax, 'Negative log-likelihood predicted by a GMM (covariance type = %s)' % cov_type,
gmm, df_data_train_scaled)
from sklearn.metrics import silhouette_score
covariance_types = ['spherical', 'diag', 'tied', 'full']
for cov_type in covariance_types:
gmm = GaussianMixture(n_components=n_classes, covariance_type=cov_type)
gmm.fit(df_data_train_scaled)
pred = gmm.predict(df_data_test_scaled)
pred_probabilities = gmm.predict_proba(df_data_test_scaled)
print(gmm)
print(silhouette_score(df_data_test_scaled, pred))
print(gmm.means_)
print("----Test data points----")
for cluster, prob in zip(pred, pred_probabilities):
print(cluster)
print(prob)
Exercise: Evaluation metrics and Spherical plots for GMM¶
A contour plot is useful for visualizing the shape of a Gaussian Mixture Model, because it shows the probability distributions for each class.
For clustering purposes, if we don't care so much about the probabilities, we can do spherical plots instead.
- Complete the
get_metricshelper function to get the evaluation metrics for each GMM covariance type. - Which model will you choose, based on the evaluation metrics?
from matplotlib.patches import Ellipse
def get_gmm_cov_matrix(gmm, label):
"""Returns the covariance matrix
Args:
gmm: the Gaussian Mixture Model
label: the label index
Returns:
the covariance matrix
Credits: http://www.stats.ox.ac.uk/~sejdinov/teaching/dmml/Mixtures.html
"""
if gmm.covariance_type == 'full':
# one per label (of any type)
cov = gmm.covariances_[label]
elif gmm.covariance_type == 'tied':
# all the same
cov = gmm.covariances_
elif gmm.covariance_type == 'diag':
# diagonal matrix per label
cov = np.diag(gmm.covariances_[label])
elif gmm.covariance_type == 'spherical':
# all spherical
cov = np.eye(gmm.means_.shape[1]) * gmm.covariances_[label]
return cov
def plot_cov_ellipse(cov, pos, color='b', ax=None, **kwargs):
"""Plots the covariance ellipse
Args:
cov: the covariance to plot
pos: the position
color: the ellipse color
ax: the subplot axis
Returns:
the ellipse
Credits: http://www.stats.ox.ac.uk/~sejdinov/teaching/dmml/Mixtures.html
"""
def eigsorted(cov):
vals, vecs = np.linalg.eigh(cov)
order = vals.argsort()[::-1]
return vals[order], vecs[:,order]
if ax is None:
ax = plt.gca()
vals, vecs = eigsorted(cov)
theta = np.degrees(np.arctan2(*vecs[:,0][::-1]))
nstd = 2 # ???
# Width and height are "full" widths, not radius
width, height = 2 * nstd * np.sqrt(vals)
ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, color=color, alpha=0.2,**kwargs)
ax.add_artist(ellip)
return ellip
from sklearn import metrics
def get_metrics(model, test_data, test_labels):
"""Returns the cluster evaluation metrics
Args:
model - the model
test_data - the test dataset
test_labels - the test labels
Returns:
a tuple of (homogeniety_score, completeness_score
v_measure_score, adjusted_rand_score, silhouette_score)
"""
# Your code here
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(20, 20),
sharex=True, sharey=True)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, n_classes)]
covariance_types = ['spherical', 'diag', 'tied', 'full']
for cov_type, ax in zip(covariance_types, axes.flatten()):
gmm = GaussianMixture(n_components=n_classes, covariance_type=cov_type)
gmm.fit(df_data_train_scaled)
ax.scatter(df_data_train_scaled[:, 0], df_data_train_scaled[:, 1],
color='black', marker='x')
homogeneity, completeness, vmeasure, adjusted_rand, silhouette = \
get_metrics(gmm, df_data_test_scaled, df_labels_test)
for label, color in enumerate(colors):
cov = get_gmm_cov_matrix(gmm, label)
position = gmm.means_[label]
plot_cov_ellipse(cov, position, color=color, ax=ax)
ax.set(title='GMM with \'%s\' covariance\n'
'homogeneity %.2f, completeness %.2f, v-measure %.2f\n'
'adjusted rand score %.2f, silhouette coefficient %.2f'
% (cov_type, homogeneity, completeness, vmeasure, adjusted_rand,
silhouette),
xticks=(), yticks=())
DBSCAN¶
The final clustering algorithm we'll look at is DBSCAN.
The key feature of DBSCAN is that it can find clusters of any shape (not just spherical or convex).
Instead of telling it how many clusters to find, DBSCAN can estimate the clusters from the data.
http://scikit-learn.org/stable/modules/clustering.html#dbscan
Walkthrough - DBSCAN on the COE dataset¶
Credits: http://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html
Data preparation¶
DBSCAN does not have the concept of 'predict'.
We'll use the "full" dataset (first 300 values), without splitting train and test.
from sklearn.preprocessing import StandardScaler
scaler_all = StandardScaler()
df_data_scaled = scaler_all.fit_transform(df_data)
Fit the model to get:
- The core samples that DBSCAN considers as part of a cluster
- The cluster labels that DBSCAN found
The eps and min_samples settings are tunable to the dataset, depending on how many clusters you would like DBSCAN to find.
More details: DBSCAN?
from sklearn.cluster import DBSCAN
# eps : float, optional
# The maximum distance between two samples for them to be considered
# as in the same neighborhood.
# min_samples : int, optional
# The number of samples (or total weight) in a neighborhood for a point
# to be considered as a core point. This includes the point itself.
db = DBSCAN(eps=0.3, min_samples=10) # these can be tuned
# based on how many clusters
# you want DBSCAN to find
db.fit(df_data_scaled)
print(df_data_scaled[db.labels_==-1])
print(df_data[db.labels_==-1])
[[ 1.11916722 0.19388856]
[ 0.21599259 0.7444446 ]
[ 1.11916722 0.54355104]
[ 0.48608754 -0.16093643]
[-0.17986084 0.41582071]
[ 0.94482022 0.42448039]]
quota premium
720 1659 45002
721 1027 54920
725 1659 51301
731 1216 38610
764 750 49000
766 1537 49156
DBSCAN?
# Number of clusters in labels, ignoring unlabeled noise / outliers
n_clusters = len(set(db.labels_)) - int(-1 in set(db.labels_))
n_clusters2 = max(set(db.labels_)) + 1
print('Estimated number of clusters: %d' % n_clusters)
print('Estimated number of clusters: %d' % n_clusters2)
Estimated number of clusters: 2 Estimated number of clusters: 2
Compute the Evaluation Metrics:
labels_true = df_labels
labels_predict = db.labels_
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels_predict))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels_predict))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels_predict))
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels_predict))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(df_data_scaled, labels_predict))
Homogeneity: 0.800 Completeness: 0.885 V-measure: 0.840 Adjusted Rand Index: 0.722 Silhouette Coefficient: 0.670
Plot the clusters found by DBSCAN:
import matplotlib.pyplot as plt
def plot_dbscan(ax, db, X, title):
"""Plots the clusters found by the DBSCAN algorithm
Args:
ax: matplotlib subplot axes
db: the fitted DBSCAN clusterer
X: the fitted data
title: title of the plot
"""
labels = db.labels_
# Get an array of zeros with the same shape and type
core_samples_mask = np.zeros_like(labels, dtype=bool)
# Mark our core samples (used for identifying clusters)
core_samples_mask[db.core_sample_indices_] = True
# Plot outliers in black, clusters in colours
black = [0, 0, 0, 1]
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
for k, color in zip(unique_labels, colors):
if k == -1: # outliers
color = black
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
ax.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(color),
markeredgecolor='k', markersize=14)
# samples that are not core samples
# black indicates they are outliers
xy = X[class_member_mask & ~core_samples_mask]
ax.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(color),
markeredgecolor='k', markersize=6)
#ax.set(title=title, xticks=(), yticks=())
fig, ax = plt.subplots(figsize=(15, 10))
plot_dbscan(ax, db, df_data_scaled,
'COE Quotas vs Premiums, Estimated number of clusters: %d' % n_clusters)
# eps : float, optional
# The maximum distance between two samples for them to be considered
# as in the same neighborhood.
# min_samples : int, optional
# The number of samples (or total weight) in a neighborhood for a point
# to be considered as a core point. This includes the point itself.
db2 = DBSCAN(eps=.4, min_samples=10)
db2.fit(df_data_scaled)
n_clusters = len(set(db2.labels_)) - int(-1 in set(db2.labels_))
# predictions
fig, ax = plt.subplots(figsize=(15, 10))
plot_dbscan(ax, db2, df_data_scaled,
'COE Quotas vs Premiums, Estimated number of clusters: %d' % n_clusters)